Выявление корреляционных связей в медико-географических исследованиях (П. П. Решетников, С. С. Панфилова, Н. И. Володина, В. А. Червяков)

Задачи, стоящие перед медицинской географией, могут быть успешно решены только в результате познания влияния на здоровье населения всего комплекса природных и социально-экономических условий конкретных территорий. Здоровье человека зависит от многих неизвестных и меняющихся факторов. Изучение всех этих факторов требует рассмотрения свойств географической среды в их взаимосвязи и непрерывном изменении. Теория корреляции (один из разделов математической статистики) позволяет объективно охарактеризовать эти связи и выразить их в количественной форме. В настоящее время статистические методы широко применяются в самых различных областях знания, в том числе и в медицине. Однако изучение влияния географической среды на здоровье населения требует специальных методов ее решения. Большую роль здесь могут сыграть географические карты, дающие наглядное и обобщенное представление о целом комплексе природных и социально-экономических условий конкретных территорий. Картографический анализ этих данных может предоставить в распоряжение исследователя большой объем количественной и качественной информации, а метод корреляции, позволит понять и оценить степень взаимозависимости отдельных показателей.

Предлагаемая работа является примером выявления корреляционных связей по географическим картам при медико-географических исследованиях. Сделана попытка изучения зависимости заболеваемости дизентерией от природных факторов Целинного края.

Известно, что на величину заболеваемости дизентерией оказывают влияние такие местные условия как уровень санитарного состояния населенных мест и жилищ, климат, обеспеченность питьевой водой и др. Изучение заболеваемости было бы полным при исследовании влияния на нее всего комплекса природных и социально-экономических условий. В данной работе прослежено влияние только двух факторов: климатического и обеспеченности питьевой водой.

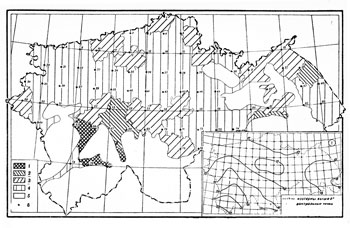
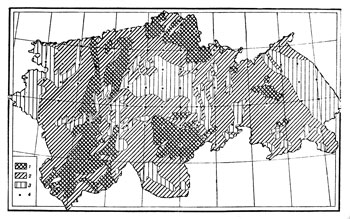
Была составлена уточненная картограмма заболеваемости дизентерией по административным районам Целинного края (рис. 1). Уточнение производилось по контурам людности населения, взятым с карты размещения населения Атласа Целинного края. (1964, стр. 41). Заболеваемость дана в условных показателях. Поскольку пик заболеваемости наблюдался в августе, то была составлена карта средних температур августа на территории Целинного края (врезка на рис. 1). Данные для нее были взяты из Климатического атласа СССР (1960, стр. 28-29). Для изучения влияния на заболеваемость обеспеченности населения питьевой водой была составлена карта степени минерализации подземных вод (рис. 2). Степень минерализации подземных вод принята нами как косвенный показатель обеспеченности питьевой водой. Показатели минерализации подземных вод взяты также из атласа Целинного края (1964, стр. 9). Для определения величин тесноты связи между интенсивностью заболеваемости дизентерией и температурой воздуха интенсивностью заболеваемости и степенью минерализации подземных вод была вычерчена сетка контрольных точек (см. карты). Ввиду того, что используемые нами карты различны по масштабам (карта заболеваемости и карта степени минерализации подземных вод - м. 1:3000000, карта средних температур м. 1:6000000) то количественные показатели легче определить в пересечениях градусной сетки. В своей работе «Особенности определения корреляционных связей по географическим картам» В. А. Червяков (1964) пришел к выводу, что число контрольных точек влияет на точность определения тесноты связей (коэффициента корреляции). Однако количество их не должно значительно превышать числа административных единиц на карте, т. к. большое число наблюдений не исключает ошибок, зависящих от степени территориальной дробности. Поэтому нами было произведено сгущение картографической сетки (контрольные точки размещались через 1° по широте и 40' по долготе). Все точки пронумерованы. На незаселенной территории наблюдения не производились. Имея вышеуказанные данные, приступили к картометрическим и вычислительным работам по определению коэффициента корреляции (г). Покажем ее на примере нахождения взаимосвязей между заболеваемостью дизентерией и температурой в августе.

Рис. 1. Уточненная картограмма заболеваемости дизентерией в Целинном крае. 1-4 - уровень заболеваемости в интенсивных показателях; 5 - незаселенные территории; 6 - контрольные точки, в которых производились измерения для статистических расчетов. На врезке показана карта температур воздуха в августе

Строим оси координат. На оси (у) откладываем интервалы интенсивности заболеваемости дизентерией, показанные на карте, на оси (x₁) - температурные интервалы через 1°. Получили сетку квадратов, так называемую корреляционную решетку (табл. 1). Следующий этап работы - заполнение клеток решетки данными картометрических наблюдений в каждой из контрольных точек. Так, например, точка № 1 входит в интервал группировки 0-20 но (у) и 16°-17° по (х). В клетке, находящейся на пересечении строки 0-20 и столбца 16-17° отмечаем точкой произведенное наблюдение.

Рис. 2. Картосхема залегания подземных вод в Целинном крае. 1 - сильно соленые; 2 - слабо соленые; 3 - пресные; 4 - контрольные точки

Аналогично производим заполнение корреляционной решетки по данным всех 80 контрольных точек. Последняя точка № 80 входит в строку интервала группировки 60-80 по (у) и 20-21° по оси (х). Подсчитываем и записываем количество наблюдений в каждой клетке корреляционной решетки. Вычисление коэффициента корреляции производилось с помощью табл. 1, которая включает и заполненную нами корреляционную решетку.

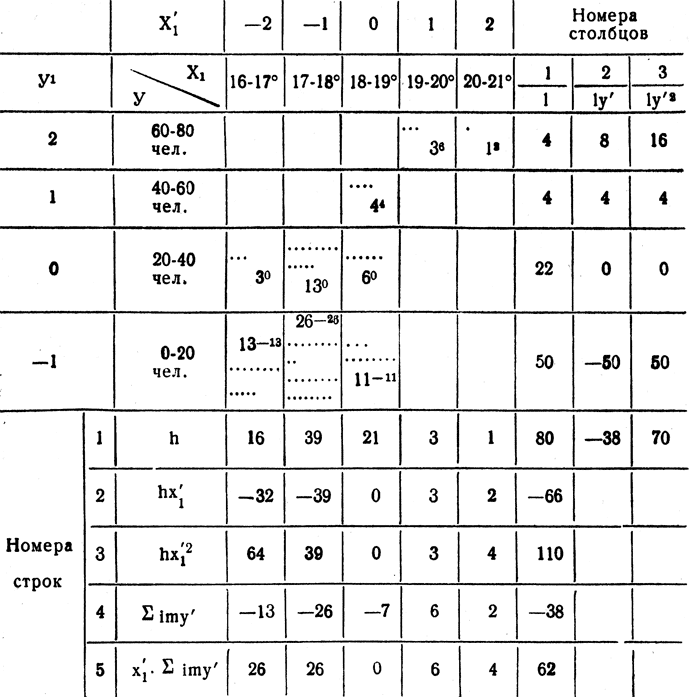
Таблица 1. Корреляционная решетка

Схема вычисления коэффициента корреляции заимствована из книги Я. И. Лукомского (1961). Заменяем значения X₁ и у упрощенными значениями х′₁ и у′, для чего обозначаем середины интервалов заболеваемости и температур последовательным рядом простых целых положительных и отрицательных чисел с нулем для среднего интервала. Это преобразование значительно облегчает последующие вычисления. В нашем примере середины интервалов по (у) будут обозначаться числами от -1 до +2 и по (х) - от -2 до +2.

Умножаем число наблюдений в каждой клетке корреляционной решетки на (у) и результаты записываем в правом верхнем углу соответствующей клетки. Затем заполняем строки 1, 2, 3, 4, 5 и столбцы 1, 2, 3. Объясним получение чисел в некоторых из них. Строка 1 (h) - сумма наблюдений по столбцам корреляционной решетки. Столбец 1 (1) - сумма по строкам. Строка 4 (∑imy′) получена суммированием по столбцам чисел, расположенных в правых верхних углах клеток. Правила заполнения остальных строк и столбцов корреляционной таблицы вполне понятны из буквенных обозначений. Находим суммы по строкам и столбцам. Коэффициент корреляции вычисляем по формуле:

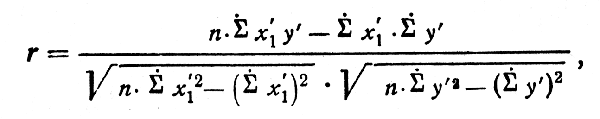
где n - число наблюдений (сумма по строке 1 или столбцу 1),

Σ′x′₁y′ - сумма по строке 5,

Σ′x′₁ - сумма по строке 2,

Σ′y′ - сумма по столбцу 2,

Σ′x′₁² - сумма по строке 3,

Σy′² - сумма по столбцу 3.

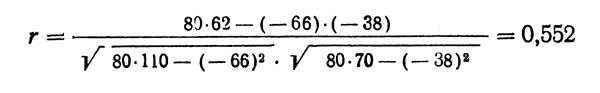
Группировки количественных данных по картам приводят к ошибкам, которые преуменьшают первоначально вычисленные показатели тесноты связи. Исследования, проведенные В. А. Червяковым (1964), показали, что при числе интервалов группировки меньше шести занижение коэффициентов корреляции может быть значительным. Им предложена упрощенная схема коррекции коэффициента корреляции. Для этого вначале вычисляются упрощенные значения средних квадратических отклонений по x₁ и у.

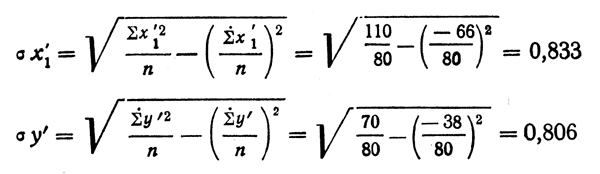
Затем производится коррекция упрощенных средних квадра-тических отклонений за интервалы группировки по формулам:

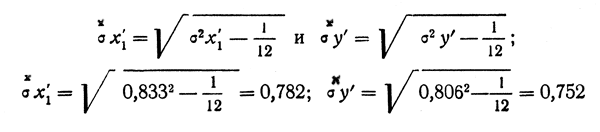
Наконец, коэффициент корреляции исправляется по формуле:

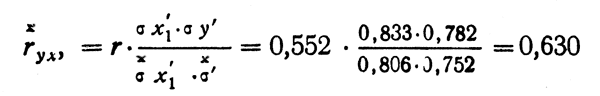
Средняя квадратическая ошибка коэффициента корреляции, характеризующая точность определения тесноты связи, вычисляется по формуле:

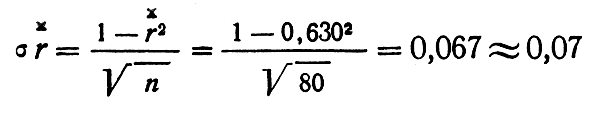
При такой точности коэффициент корреляции можно округлить до сотого знака. Результаты вычисления коэффициента корреляции и его средней квадратической ошибки обычно записываются в следующем виде:

r_xy1 = 0,63 ± 0,07

При недостаточном числе наблюдений или при малой величине коэффициента корреляции приходится сомневаться в реальности существания связи между изучаемыми явлениями. Достоверность связи определяется отношением абсолютной величины коэффициента к его средней квадратической ошибке. Если

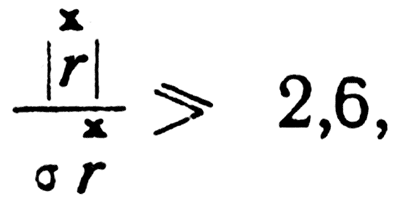
то связь можно считать достоверной (Лукомский, 1961). Если это отношение меньше 2,6, то связи возможно и нет. В нашем примере зависимость между заболеваемостью дизентерией и температурами в августе вполне достоверна, т. к. 0,63/0,07 = 9, что значительно превышает число 2,6.

Коэффициент корреляции между заболеваемостью дизентерией и степенью минерализации подземных вод (см. рис. 1, 2) оказался равным r_yx2 = 0,38±0,10. Он значительно меньше коэффициента корреляции между интенсивностью изучаемой заболеваемости и температурами в августе (r_yx1 = 0,63).

Картографический анализ, таким образом, дает возможность выявить те общие эпидемиологические закономерности, которые свойственны данной инфекции. Но, как правило, изучаемое явление всегда в большей степени зависит от совокупности рассматриваемых факторов, чем от каждого из них в отдельности. Корреляционные методы позволяют определить и совокупное воздействие их, которое количественно выражается коэффициентом множественной корреляции (R). С вовлечением большого числа факторов все точнее будет определяться теснота связи поучаемых явлений, а величина (R) будет приближаться к единице.

Так как данная работа имеет методический характер, мы не делаем выводов относительно сущности взаимосвязей изучаемых явлений. Однако уже из вышесказанного видно, что картографический способ определения корреляционных связей открывает новые возможности медико-географических исследований. Получить признание этот метод может только при более широком применении его в исследовательской работе.

Литература

Атлас Целинного края, М., ГУГК, 1964.

Климатический Атлас СССР М., ГУГК, I960, т. 1.

Лукомский Я. И. «Теория корреляции и ее применение к анализу» М., Госстатиздат, 1961.

Червяков В. А. «Особенности определения корреляционных связей по геоографическим картам». Канд. диссерт. МГУ, 1964.

Москва. Институт эпидемиологии и микробиологии им. Н. Ф. Гамалеи АМН СССР